Shaky Solution Resolved

Okay, so the solution to the triangle problem is shaky because there are multiple ways of forming the same set of segments. Consider breaking a line segments into three different sized pieces: one short, one medium, and one long, and call each one a, b, and c respectively. There are six possible arrangements of these three segments to make the original:
abc, acd, bac, bca, cab, and cba
Fortunately, the equilateral triangle solution offered before also gives six arrangements for any set of three distinct segments. For example, in the picture shown below each dot gives six identical sets of three segments (well, approximately identical, since I am no graphic artist).

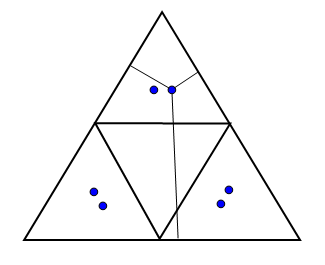
So it was not enough that the sum of the segments is constant and that there were arrangements for all possible sizes; there had to be the same multiplicity of arrangements, which, conveniently, there was.

A more straightforward solution can be achieved using simple algebra and graphing. Let the arbitrary original segment have a length of 1 unit. Let the first of the three segments it is broken into have length x, the second have length y, and the third have length (1 – x – y).
All possibilities are given by the area in the solution to the three inequalities x > 0, y > 0, and x + y < 1 (superfluous are x <1 and y < 1 because x + y < 1)


Okay, so now we consider what region of this area makes a triangle possible, or, as is common in probability problems, what makes a triangle not possible. To make a triangle none of the segments can be longer than the other two put together. In this problem, where we start with a segment that has a length of 1 unit, we cannot let any of the pieces be longer than 1/2 a unit, or it will be longer than the other two combined, and a triangle cannot be formed. This gives the following three inequalities for what each piece can be:
x < ½, y < ½, and x + y > ½ (from the inequality for the third side: 1 – x – y < ½) This gives the region in yellow in the picture below:

And once again it is clear (but now even clearer) that the probability is 25%. Funny how a similar picture results from a completely different process…

There is another creative approach to solving this problem that I found. It involves bending the segment to make a circle and considering which placements of the two breaking points on the circle-segment will work. I’ll post this sometime in the future.

Like this problem? Try the next one that it leads to. If you break a line segment into 4 pieces, what is the probability that you can make a quadrilateral?
Still having fun? How about if you break a segment into n-pieces?
I’ll revisit these.