A Beautiful but Shaky Solution

There is something so good feeling about finding a simple and elegant solution to a difficult problem in mathematics. Indeed, it is most impressive in any field when someone can make abstruse concepts understandable to people who are not experts in the field (Richard Feinman is famous for this).
If the solution or explanation is faulty or incomplete, however, the supplier has done a disservice that can outweigh whatever good might have come giving the correct answer. It is still more frustrating is if the wrongly-reasoned conclusion happens to lead to the correct result. This allows the misconception to be perpetuated.
A great example is the following “solution” to a famous math problem. It does work, but there are some dangerous assumptions (or overlooked details) that can lead someone astray if they tried to use a similar method for a different problem. Here it goes.

Question: If you randomly break a line segment twice, what is the probability that you can make a triangle from the three resulting segments?

Solution: Start by inscribing an equilateral triangle inside a larger equilateral triangle as shown below:



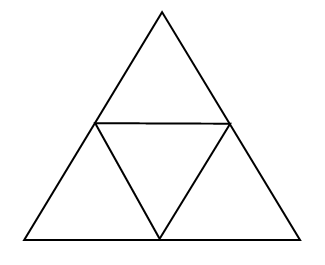
Now pick a point anywhere in the big triangle, and draw three segments connecting the point to each side of the big triangle at perpendicular angles. Wherever you pick a point, the sum of the drawn segments is always the same (for instance, sum=sqrt(3), if each small triangle's side length is 1 unit) so they can represent three segments we get from randomly cutting some segment twice (as stated in the original question). Look below:


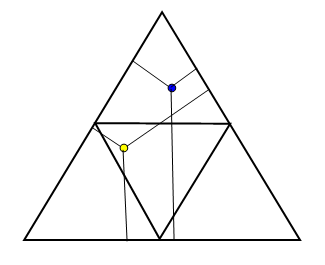
If the chosen point is in the center equilateral triangle (like the yellow dot), then you can make a triangle from the three segments. If it is in one of the other three small trangles (like the blue dot), then you cannot make a triangle from the segments. Since the center triangle’s area is 25% of the total area, the probability of being able to make a triangle is also 25%.


Okay, so it is true that the probability is 25%, but can you find it by alternate means? Can you explain what is shaky about this solution?

I’ll post other solutions in one week.