Poetry and Math: moments and removable discontinuities

Below is one of my favorite poems.

This Much I Do Remember:

It was after dinner.
You were talking to me across the table
about something or other,
a greyhound you had seen that day
or a song you liked,

and I was looking past you
over your bare shoulder
at the three oranges lying
on the kitchen counter
next to the small electric bean grinder,
which was also orange,
and the orange and white cruets for vinegar and oil.

All of which converged
into a random still life,
so fastened together by the hasp of color,
and so fixed behind the animated
foreground of your
talking and smiling,
gesturing and pouring wine,
and the camber of your shoulders

that I could feel it being painted within me,
brushed on the wall of my skull,
while the tone of your voice
lifted and fell in its flight,
and the three oranges
remained fixed on the counter
the way stars are said
to be fixed in the universe.

Then all the moments of the past
began to line up behind that moment
and all the moments to come
assembled in front of it in a long row,
giving me reason to believe
that this was a moment I had rescued
from the millions that rush out of sight
into the darkness behind the eyes.

Even after I have forgotten what year it is,
my middle name,
and the meaning of money,
I will still carry in my pocket
the small coin of that moment,
minted in the kingdom
that we pace through every day.

--Billy Collins

A moment is such a hard thing to define. Does it have any length, or only position relative to moments before and after it?
A removable discontinuity in mathmatics and a moment in time have some similar attributes. Take the function graphed below that has a R.D. at x = 2.


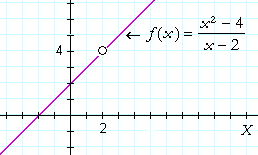We see that even thought there is a small circle marking the discontinuity at (2,4), actually the point has no dimension and thus the discontinuity has location but not length.
If you have taken math past Algebra II, the picture above is probably (I hope!) somewhat familiar, but maybe not all that interesting. Recall this part of the poem:
"Then all the moments of the past
began to line up behind that moment
and all the moments to come
assembled in front of it in a long row"

Too bad mathematics courses so rarely try to build on such beautiful connections like this.

Lumps in the Batter of Mixed Metaphors

This entry will actually cover three topics: defining metaphor, mixed metaphors, and dormant metaphors.
Before discussing the use and abuse of metaphors, it is worth clarifying the definition of metaphor. A metaphor is a figure of speech that directly calls one thing something else, or says that it is that other thing. In grade-school our teachers did a great job of helping us distinguish between simile and metaphor, the former using like or as and being explicit, the latter being implicit. Unfortunately, analogies are not contrasted with metaphors enough.
An analogy is a similarity (or a comparison based on a similarity) between two things that are otherwise dissimilar. While similes, metaphors and analogies all extend meaning through correspondence, typically metaphors and similes give elegant depth to a description, while analogies give practical understanding. This is why analogies are a central tool in teaching and explaining.
Yet too frequently people incorrectly call analogies metaphors. Usually these infractions begin with the phrase “A good metaphor for … is …”.
For example, “A good metaphor for the stages of intimacy with someone is rounding the bases to score a run in baseball.” This is actually an analogy, and an overworked and generally lame one at that. Try to fill the … in the phrase with an example of a metaphor. Semantically this construction is perilous. A safer approach is to start “A good metaphor is …”. Just say the metaphor—then describe it.

Unless being used for purposeful humor (like the title of this posting), mixed metaphors are embarrassing mistakes that leave readers either confused or laughing at (instead of with) the writer. One of my favorites is in a speech by a scientist who referred to “a virgin field pregnant with possibilities.”
Clichés can also spin out of control: “They’ll be watching everything you do with fine-toothed comb.” Sorry, combs can’t watch anything.
A truly amazing foul up is when two expressions are mixed together incorrectly and the result takes on a whole new (and unintended) meaning beyond the confused parts. The website http://www.stuntmonkey.com/metaphor/ calls this a triple wammy. The following is my favorite: “We’re starting from ground zero.” This confuses “starting from square-one/the beginning/zero”, with “building from the ground-up,” to result in dealing with a nuclear attack. Remarkable!

Finally, a dormant metaphor is somewhat like a Freudian slip. It occurs when the literal meaning of the metaphorical language infringes on its extended purpose. This comes from poor contextual placement. For instance, consider this sentence taken from a law journal: “This note examines the doctrine set forth in Roe v. Wade and its progeny.” Since progeny literally means offspring, this is probably not the most appropriate place to use it more loosely referring to a result or product.
On a subtler note, the vehicle (i.e. literal sense of the metaphorical language) should harmonize with the tenor (i.e. intended metaphorical sense) of a metaphor. For instance, “the internet superhighway” makes sense because both highways and the internet are modern technological achievements. “The internet super-trail” falls flat.
However, sometimes the discord is purposeful and effective, as in “concrete jungle”.

Please send in comments with some of your own favorite uses and abuses of metaphors.

Shaky Solution Resolved

Okay, so the solution to the triangle problem is shaky because there are multiple ways of forming the same set of segments. Consider breaking a line segments into three different sized pieces: one short, one medium, and one long, and call each one a, b, and c respectively. There are six possible arrangements of these three segments to make the original:
abc, acd, bac, bca, cab, and cba
Fortunately, the equilateral triangle solution offered before also gives six arrangements for any set of three distinct segments. For example, in the picture shown below each dot gives six identical sets of three segments (well, approximately identical, since I am no graphic artist).

So it was not enough that the sum of the segments is constant and that there were arrangements for all possible sizes; there had to be the same multiplicity of arrangements, which, conveniently, there was.

A more straightforward solution can be achieved using simple algebra and graphing. Let the arbitrary original segment have a length of 1 unit. Let the first of the three segments it is broken into have length x, the second have length y, and the third have length (1 – x – y).
All possibilities are given by the area in the solution to the three inequalities x > 0, y > 0, and x + y < 1 (superfluous are x <1 and y < 1 because x + y < 1)


Okay, so now we consider what region of this area makes a triangle possible, or, as is common in probability problems, what makes a triangle not possible. To make a triangle none of the segments can be longer than the other two put together. In this problem, where we start with a segment that has a length of 1 unit, we cannot let any of the pieces be longer than 1/2 a unit, or it will be longer than the other two combined, and a triangle cannot be formed. This gives the following three inequalities for what each piece can be:
x < ½, y < ½, and x + y > ½ (from the inequality for the third side: 1 – x – y < ½) This gives the region in yellow in the picture below:

And once again it is clear (but now even clearer) that the probability is 25%. Funny how a similar picture results from a completely different process…

There is another creative approach to solving this problem that I found. It involves bending the segment to make a circle and considering which placements of the two breaking points on the circle-segment will work. I’ll post this sometime in the future.

Like this problem? Try the next one that it leads to. If you break a line segment into 4 pieces, what is the probability that you can make a quadrilateral?
Still having fun? How about if you break a segment into n-pieces?
I’ll revisit these.

A Beautiful but Shaky Solution

There is something so good feeling about finding a simple and elegant solution to a difficult problem in mathematics. Indeed, it is most impressive in any field when someone can make abstruse concepts understandable to people who are not experts in the field (Richard Feinman is famous for this).
If the solution or explanation is faulty or incomplete, however, the supplier has done a disservice that can outweigh whatever good might have come giving the correct answer. It is still more frustrating is if the wrongly-reasoned conclusion happens to lead to the correct result. This allows the misconception to be perpetuated.
A great example is the following “solution” to a famous math problem. It does work, but there are some dangerous assumptions (or overlooked details) that can lead someone astray if they tried to use a similar method for a different problem. Here it goes.

Question: If you randomly break a line segment twice, what is the probability that you can make a triangle from the three resulting segments?

Solution: Start by inscribing an equilateral triangle inside a larger equilateral triangle as shown below:



Now pick a point anywhere in the big triangle, and draw three segments connecting the point to each side of the big triangle at perpendicular angles. Wherever you pick a point, the sum of the drawn segments is always the same (for instance, sum=sqrt(3), if each small triangle's side length is 1 unit) so they can represent three segments we get from randomly cutting some segment twice (as stated in the original question). Look below:


If the chosen point is in the center equilateral triangle (like the yellow dot), then you can make a triangle from the three segments. If it is in one of the other three small trangles (like the blue dot), then you cannot make a triangle from the segments. Since the center triangle’s area is 25% of the total area, the probability of being able to make a triangle is also 25%.


Okay, so it is true that the probability is 25%, but can you find it by alternate means? Can you explain what is shaky about this solution?

I’ll post other solutions in one week.

Nuanced Intensifiers

The English language has many wonderful intensifiers. This gives the able speaker or writer the ability to be acutely specific. This is why the word very is so dreaded—it has no flavor. Just like flavors, though, intensifiers can taste bad if combined improperly.
A word that comes to mind is highly. Highly is frequently substituted for a simpler adjective to give some loftiness (figuratively speaking, that is) to another adjective. “Highly intelligent” is perhaps the most common and clichéd, but at least it makes sense. Examples of less logical uses abound. For instance, one hears of “highly unmotivated students” (especially these days). How about “heavily unmotivated students”? Doesn’t that sound a bit more accurate? Sadly, a Google search retrieves 514 hits for “highly unmotivated,” and only 12 for “heavily unmotivated”.
Another example involves discounts. “Highly discounted” is an especially illogical and unappealing advertisement. Once again, “heavily discounted” rings much truer. Fortunately, businesses have caught on to this one as “heavily discounted” gets 495,000 hits compared to only 191,000 for “highly discounted”.
Here are some other nuanced pairs of intensifiers to consider:

particularly and especially
quite and very
considerably and significantly
severely and tragically